Función Cuadrática ( Teoría )

Explicación:

Procedemos al estudio de la función cuadrática que en realidad no es mas que una función polinomica de segundo grado, en donde si recordamos su "Dominio = R", es decir todo el conjunto de los números reales.

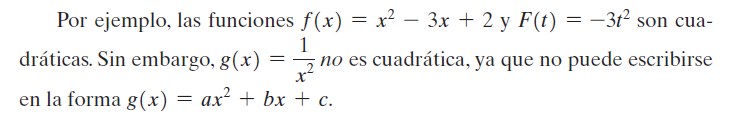
En los ejemplos podemos apreciar tres funciones las dos primeras son cuadráticas mientras que la tercera no lo es ¿ por que ? simplemente por que la variable o literal ( es decir la X ) esta en el denominador, en realidad es una función racional por ello no es cuadrática.

La función cuadrática genera una parábola o curva en el plano cartesiano como lo podemos apreciar, la concavidad ( si abre hacia arriba o hacia abajo ) la determinara el signo del coeficiente ( numero ) que acompaña al literal ( variable o letra) que esta elevada al grado 2 ( al cuadrado ), en conclusión si el numero que acompaña a la letra de grado 2 es positiva ( + ) la parábola habré hacia arriba ( concavidad positiva ) mientras que si el numero que acompaña a la letra de grado 2 es negativa ( - ) la parábola abrirá hacia abajo.

Para esta función solo nos interesara su vértice ( donde se origina la parábola ), intersecciones en el eje X ( Raíces ) y la intersección en el eje Y.

Para hallar el vértice haremos uso de esta formula:

Recordemos que el vértice es una coordenada de dos valores uno en el eje X y otro en el eje Y es decir V= (X,Y), esta formula nos garantiza encontrar el valor de X así que solo nos falta el de Y, que encontramos evaluando en la función inicial al valor que determinemos al usar esta formula, por ello es que esta representado de esta forma:

2. Para hallar sus raíces o intersecciones en el eje X simplemente hay que factorizar la expresión utilizando el método apropiado para ello.

3. Finalmente para encontrar la intersección con el eje Y evaluamos la función inicial a "0", ¿ por que a 0? por que el decirle a la función que el valor de X = 0 te dará su valor correspondiente en Y es decir ¿si te propongo 0 de X cual es mi valor de Y? ( 0,? ) la función te la dará.